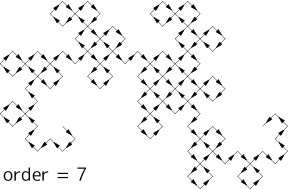Asymptoteで再帰曲線

和田先生のパラメトロン計算機: 再帰曲線を見て、Asymptoteでも再帰曲線を書きたくなった。
それぞれの曲線描画アルゴリズムは『Javaによるアルゴリズム事典』で勉強して既知なので、掲載されている何々曲線を適当に選んで、プログラミングした。
はてな記法では、Asymptoteの色付けには対応していないようなので、便宜上Cの色付けを使う。

hilbert曲線

平面を埋め尽くすように配置される曲線。

// hilbert curve

int order = 7;

int size = 512;
size(size);
real h = size / 2;
pair xy = (0, 0);

void rightUpLeft(int i);
void downLeftUp(int i);
void leftDownRight(int i);
void upRightDown(int i);

void lineTo(real dx, real dy) {
    draw((xy.x, xy.y)--(xy.x + dx, xy.y + dy));
    xy = (xy.x + dx, xy.y + dy);
}

downLeftUp = new void(int i) {
    if(i <= 0) return;
    leftDownRight(i - 1);
    lineTo(0, -h);
    downLeftUp(i - 1);
    lineTo(-h, 0);
    downLeftUp(i - 1);
    lineTo(0, h);
    rightUpLeft(i - 1);
};

leftDownRight = new void(int i) {
    if(i <= 0) return;
    downLeftUp(i - 1);
    lineTo(-h, 0);
    leftDownRight(i - 1);
    lineTo(0, -h);
    leftDownRight(i - 1);
    lineTo(h, 0);
    upRightDown(i - 1);
};

upRightDown = new void(int i) {
    if(i <= 0) return;
    rightUpLeft(i - 1);
    lineTo(0, h);
    upRightDown(i - 1);
    lineTo(h, 0);
    upRightDown(i - 1);
    lineTo(0, -h);
    leftDownRight(i - 1);
};

rightUpLeft = new void(int i) {
    if(i <= 0) return;
    upRightDown(i - 1);
    lineTo(h, 0);
    rightUpLeft(i - 1);
    lineTo(0, h);
    rightUpLeft(i - 1);
    lineTo(-h, 0);
    downLeftUp(i - 1);
};

rightUpLeft(order);

以下、全ての描画にこのlineTo関数を用いているのだが、関数の中で線を引く度にペン位置を表すpair xyが更新されるので、破壊的。pathとペン位置をreturnすれば綺麗に書けるかもしれない。

dragon曲線

有限長のテープを折り曲げて出来る曲線。

// dragon curve

int order = 7;
pair xy = (0, 0);

void lineTo(real dx, real dy) {
    draw((xy.x, xy.y)--(xy.x + dx, xy.y + dy), arrow=MidArrow);
    xy = (xy.x + dx, xy.y + dy);
}
void drawDragon(int i, real dx, real dy, int sign) {
    if(i == 0) {
        lineTo(dx, dy);
        return;
    }
    drawDragon(i - 1, (dx - sign * dy) / 2, (dy + sign * dx) / 2, 1);
    drawDragon(i - 1, (dx + sign * dy) / 2, (dy - sign * dx) / 2, -1);
}
drawDragon(order, 200, 0, 1);

hilbert曲線に比べれば短いコードだが、drawDragonで再帰している引数の変化について理解に多少時間がかかった。直線の向きを表現するために、矢印を加えている。

C曲線

Cの形をした曲線。

// c curve

int order = 10;
pair xy = (0, 0);

void lineTo(real dx, real dy) {
    draw((xy.x, xy.y)--(xy.x + dx, xy.y + dy));
    xy = (xy.x + dx, xy.y + dy);
}
void drawC(int i, real dx, real dy) {
    if(i == 0) {
        lineTo(dx, dy);
        return;
    }
    drawC(i - 1, (dx + dy) / 2, (dy - dx) / 2);
    drawC(i - 1, (dx - dy) / 2, (dy + dx) / 2);
}
drawC(order, 200, 0);

dragon曲線の折り目がちょっと違うだけといった感じで、コードも似ている。

Koch曲線

フラクタルについて教科書で学ぶと、例の2番目くらいに出てくる図。

// koch curve

int order = 7;
pair xy = (0, 0);

real[] COS;
real[] SIN;

for(int j = 0; j < 6; ++j) {
    COS.push(cos(j * pi / 3));
    SIN.push(sin(j * pi / 3));
}

void lineTo(real dx, real dy) {
    draw((xy.x, xy.y)--(xy.x + dx, xy.y + dy));
    xy = (xy.x + dx, xy.y + dy);
}
void drawKoch(int i, real d) {
    if(d <= order) {
        lineTo(d * COS[i % 6], d * SIN[i % 6]);
        return;
    }
    d = d / 3;
    drawKoch(i, d);
    ++i;
    drawKoch(i, d);
    i = i + 4;
    drawKoch(i, d);
    ++i;
    drawKoch(i, d);
}
drawKoch(0, 512);

SIN/COSはその都度計算させることも出来るが、『Javaによるアルゴリズム事典』でそうなっているように、予め表を作っておけば参照するだけなので楽になる。

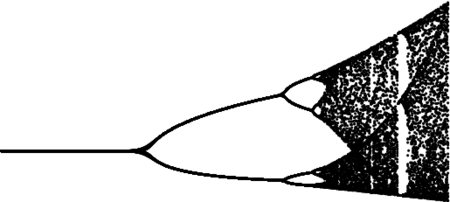
Chaos

上に並べた曲線とは少々気色が違うが、再帰的な特徴が現れる。

// chaos

int width = 512;
int height = 256;

real k_min = 1.5;
real k_max = 3.0;
real p_min = 0;
real p_max = 1.5;

for(int ik = 0; ik < width; ++ik) {
    real k = k_min + (k_max - k_min) * ik / width;
    real p = 0.3;
    for(int j = 0; j <= 50; ++j)
        p += k * p * (1 - p);
    for(int j = 51; j <= 100; ++j) {
        real ip = (p - p_max) / (p_min - p_max) * height + 0.5;
        dot((ik, ip));
        p += k * p * (1 - p);
    }
}

終わりに

Asymptoteについては、Asymptote - TeX Wiki辺りを見てもらえば、すぐに使えるようになるだろう。
ほとんど、TeXユーザのためのベクタグラフィックス記述環境だが、こうやってプログラムをして図を描画出来るというのは、実にありがたい。Processingで書いて保存という方法では手間が多い。
しかし、Ubuntu等でインストールされるデフォルトのpTeX環境がUTF-8に対応していないという現状は、宣伝する側には少し痛い。